RNN-Learn

本文使用的图片以及公式参考自Andrew Ng Deep Learning的课程。

• 简单的RNN
  • RNN Cell
  • RNN Forward
• LSTM
  • LSTM Cell
  • LSTM Forward
• 反向传播
  • RNN Cell Backward
  • LSTM Cell Backward

简单的RNN

RNN Cell

RNN包含多种结构，包括多对一，多对对，一对多，一对一。下面以一对一的结构为例来理解RNN的计算过程。文章中的代码以伪码的形式给出了核心公式的代码实现。

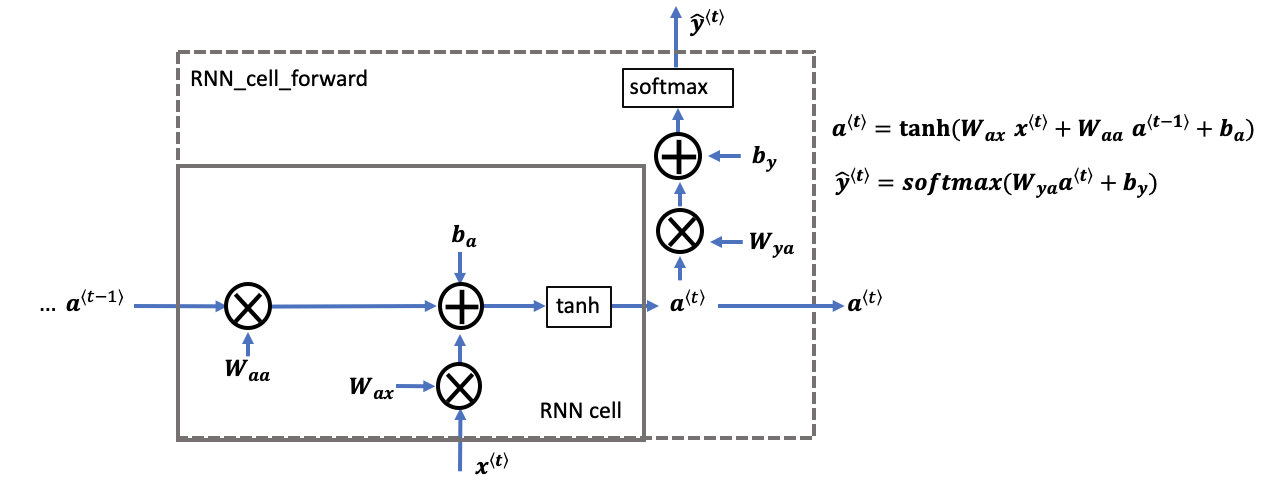
这里考虑一种简单的RNN结构，即一对一的RNN结构。在每个时间步上RNN Cell的输入有上一个时间步的激活值\(a^{<t-1>}\)和当前时间步的输入值\(x^{<t>}\)。每个时间步上的RNN Cell需要计算出当前时间步的激活值\(a^{<t>}\)和当前时间步的输出值\(\hat{y}^{<t>}\)。公式和核心伪码如下： \(a^{\langle t \rangle} = \tanh(W_{aa} a^{\langle t-1 \rangle} + W_{ax} x^{\langle t \rangle} + b_a) \tag{1.1}\)

"""
Waa: (n_a, n_a)
Wax: (n_a, n_x)
a_prev_t: (n_a, m)
a_next: (n_a, m)
x_prev_t: (n_x, m)
ba: (n_a, 1)
Wya: (n_a, n_a)
by: (n_a, 1)

m 表示batch size
"""
a_next = np.tanh(np.dot(Waa, a_prev_t) + np.dot(Wax, x_prev_t) + ba)
y_hat_t = np.softmax(np.dot(Wya, a_next)+ by)

RNN Forward

当单个RNN Cell构建完成后，就可以构建多步RNN和多隐层RNN，这里以单隐层RNN为例构建多步一对一的RNN，图示如下：

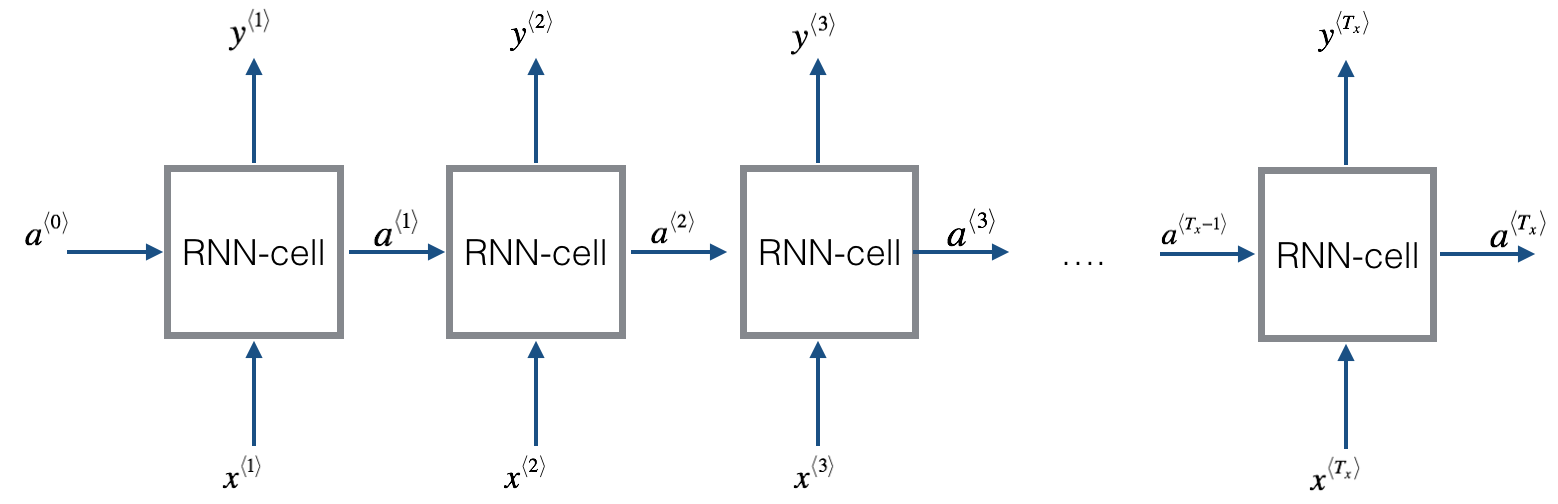
在此单隐层的RNN结构中，直接通过循环就可以完成每个时间步的计算。

"""
Input: X, a0

X: (n_x, m, T_x)。m表示batch size，T_x表示时间步的个数
a0: (n_a, m)。a0仅仅是第0个时间步的输入，因此它没有时间步这个维度
"""
input x, a0
a = np.zeros((n_a, m, T_x))
y_pred = np.zeros((n_a, m, T_x))
for t in range(T_x):
    # run_cell_forward单步rnn的前向传播。
    a_next, y_pred = rnn_cell_forward(x[:, :, t], a_next)
    # 记录anext 和y_pred
    a[:, :, t] = a_next
    y_pred[:, :, t] = y_pred

这基本上就是一个简单的RNN的前向过程，当然，RNN的结构包括多对一，一对一，一对多，多对多等结构，此外，RNN还可以设置多个隐藏层，这里仅仅使用了一个隐藏层，不过过程都是类似的。最重要的在于单步RNN的计算。

Note： 像这样的简单的RNN可以应付一些简单的文本任务，但是这样的RNN仍然存在问题。

• 上述简单的RNN，每个y_pred_t都仅仅依赖于第t时间步以及t时间步之前的内容。此外，它很难对很远的输入产生依赖，因为这里存在着梯度消失的问题。因此，这样简单的RNN仅仅适用标签词依赖于局部语境的情况。
• 两一个问题就是这样的RNN存在着梯度消失的问题。为了解决梯度消失的问题，出现了如GRU，LSTM等模型，实际上，GRU可以理解成对LSTM的一种简化。

LSTM

LSTM Cell

下图是LSTM的基本构建模块的前向和反向传播过程：

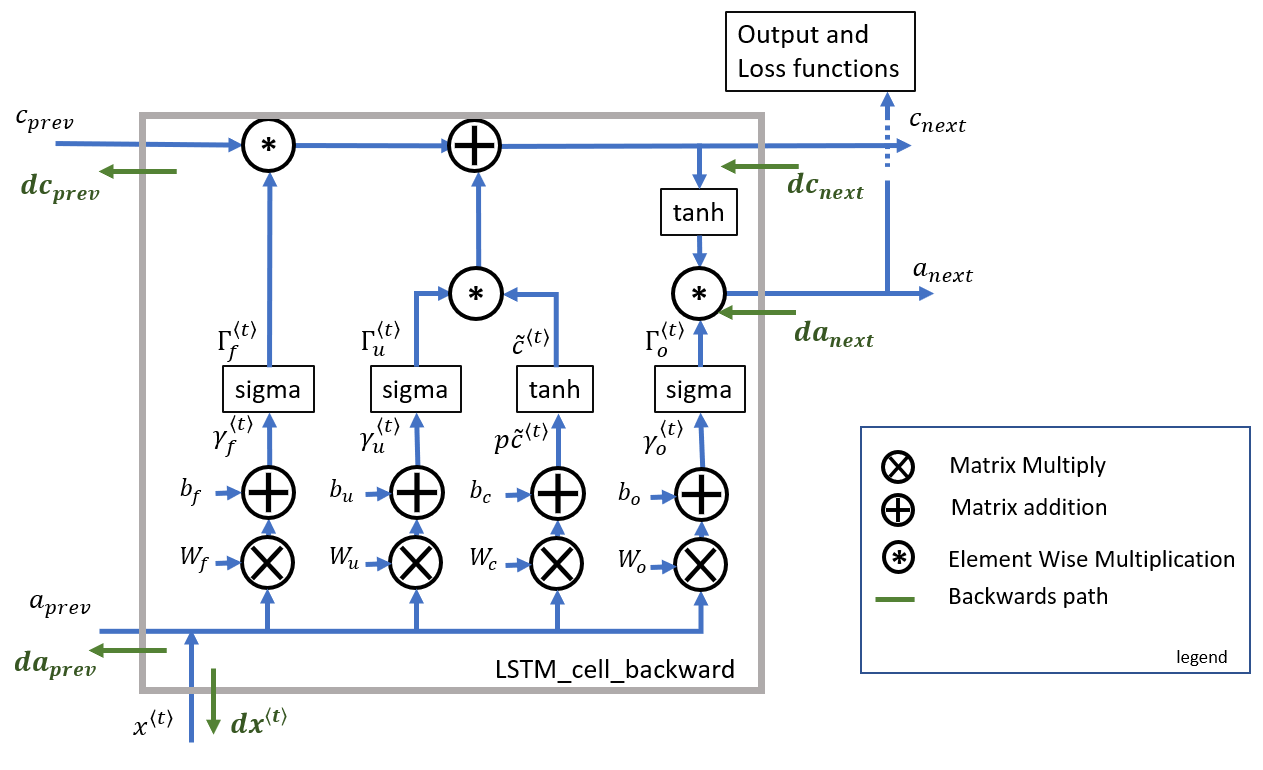
矩阵形状：

• \(a^{<t-1>}\)：(n_a, m)。上一次的激活值
• \(x^{<t>}\)：(n_x, m)。t步的输入
• \(\mathbf{W}_f\)：(n_a, n_a + n_x)。遗忘门权重
• \(b_f\)：(n_a, 1)。遗忘门偏置
• \(\mathbf{\Gamma}_f\)：(n_a, m)。遗忘门
• \(c^{<t>},c^{<t-1>},\tilde{c}^{<t>}\)：(n_a, m)。本步的门状态，上一步门状态，本步的候选门
• \(\mathbf{W}_i\)：(n_a, n_a + n_x)。更新门权重
• \(b_i\)：(n_a, 1)。更新门偏置。
• \(\mathbf{\Gamma}_i\)：(n_a, m)。更新门。
• \(\mathbf{W}_c\)：(n_a, n_a + n_x)。候选门权重。（我喜欢称为状态门）
• \(b_c\)：(n_a, 1)。候选门偏置
• \(\mathbf{W}_o\)：(n_a, n_a + n_x)。输出们权重
• \(b_o\)：(n_a, 1)。输出门偏置
• \(\mathbf{\Gamma}_o\)：(n_a, m)。输出门
• \(a^{<t>}\)：(n_a, m)。输出的激活值

遗忘门

• 将前一个状态的输出\(a^{<t-1>}\)和当前时间步的输入\(x^{<t>}\)组合一下，然后乘以权重矩阵\(\mathbf{W}_f\)再加上偏置项，然后通过sigma激活函数进行激活就得到了遗忘门的值。遗忘门是个矩阵，它的形状一定同\(c^{<t-1>}\)相同，一方面是因为该门要控制是否对之前的c值进行遗忘，因此它要控制每个c值，另一位是因为它要和\(c^{<t-1>}\)做元素乘积。

更新门

• 更新门和遗忘门的工作原理类似，都是先将上一步的激活值和本步的输入值组合一下，然后用矩阵做一下线性变换再加上偏置，最后计算激活值。值得注意的是更新门的形状和状态门的形状也是一样的。

候选状态

• 同其他门的工作原理类似，先将上一步的激活值和本步的输入值组合一下，然后用矩阵做一下线性变换再加上偏置，最后计算激活值。不同的地方在于候选状态的激活函数使用的是tanh。的候选门的形状和状态门的形状也是一样的。

状态门

• 本步的状态是通过在遗忘门和更新门的控制下融合之前的状态和本步的候选状态得到的。这里反映了LSTM的一个特点，即遗忘门和更新门独立了起来。

输出门

• 同其他门的工作原理类似，先将上一步的激活值和本步的输入值组合一下，然后用矩阵做一下线性变换再加上偏置，最后计算激活值。值得注意的是输出门的形状和状态门的形状也是一样的。

激活值

• 在输出门的控制下，使用tanh激活函数激活本步的状态值就得到了激活值。

伪码

"""
Input: xt, a_prev, c_prev
"""

concat = np.concatenate((a_prev, xt), axis=0)
ft = np.sigmoid(np.dot(Wf, concat) + bf)
it = np.sigmoid(np.dot(Wi, concat) + bi)
cct = np.tanh(np.dot(Wc, concat) + bc)
c_next = ft * c_prev + it * cct
fo = np.sigmoid(np.dot(Wo, concat) + bo)
a_next = fo * np.tanh(c_next)

LSTM Forward

将LSTM的基本构建模块连接起来就形成了LSTM网络，下面是一个单隐层的LSTM网络示意图：

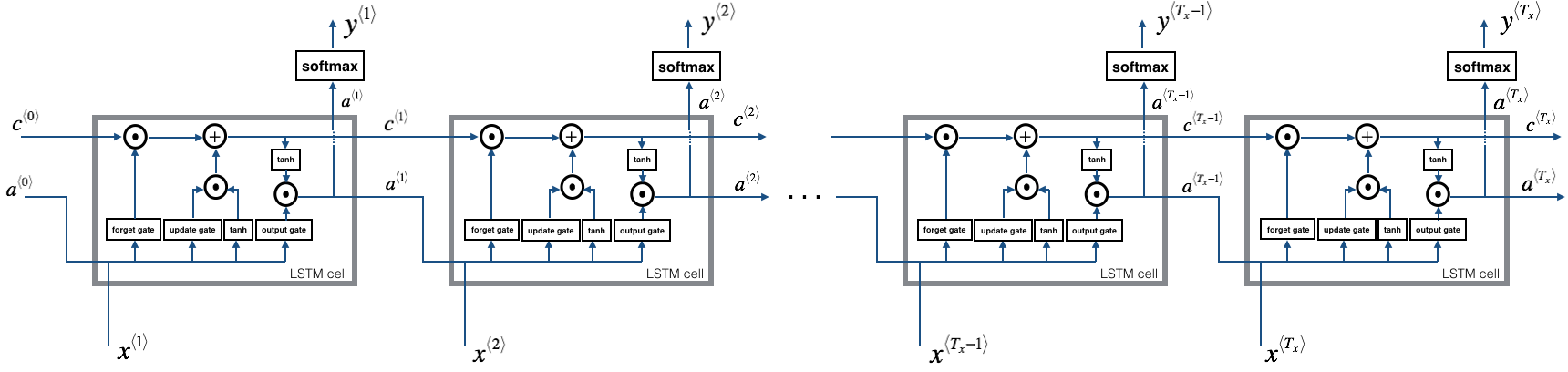
对于此单隐层的LSTM模型，我们只需要通过迭代时间步即可实现前向传播，其实，最核心的部分还是单个LSTM构建模块的内容，下面是伪码实现：

"""
Input: x, a0

"""
# 初始化变量，因为在Coursera所提供的实现方法下，反向传播需要这些变量
a = np.zeros((n_a, m, T_x))
c = np.zeros((n_a, m, T_x))
y = np.zeros((n_y, m, T_x))
a_next = a0 # a0一般为0，也可以随机初始化。
c_next = np.zeros((n_a, m))

for t in range(T_x):
    xt = x[:,:,t]
    a_next, c_next, yt, cache = lstm_cell_forward(xt, a_next, c_next, parameters)
    a[:,:,t] = a_next
    c[:,:,t]  = c_next
    y[:,:,t] = yt

反向传播

下面只关注RNN Cell和LSTM Cell的反向传播，因为现有的深度学习框架使得我们不必关注反向传播的细节。但是我觉得，这里的反向传播的计算对于理解神经网络利用标量对矩阵的求导来进行反向传播的机制是很有意义的。它也有助于理解自动求导的机制。

RNN Cell Backward

下图是RNN Cell前向传播和反向传播的过程示意图。

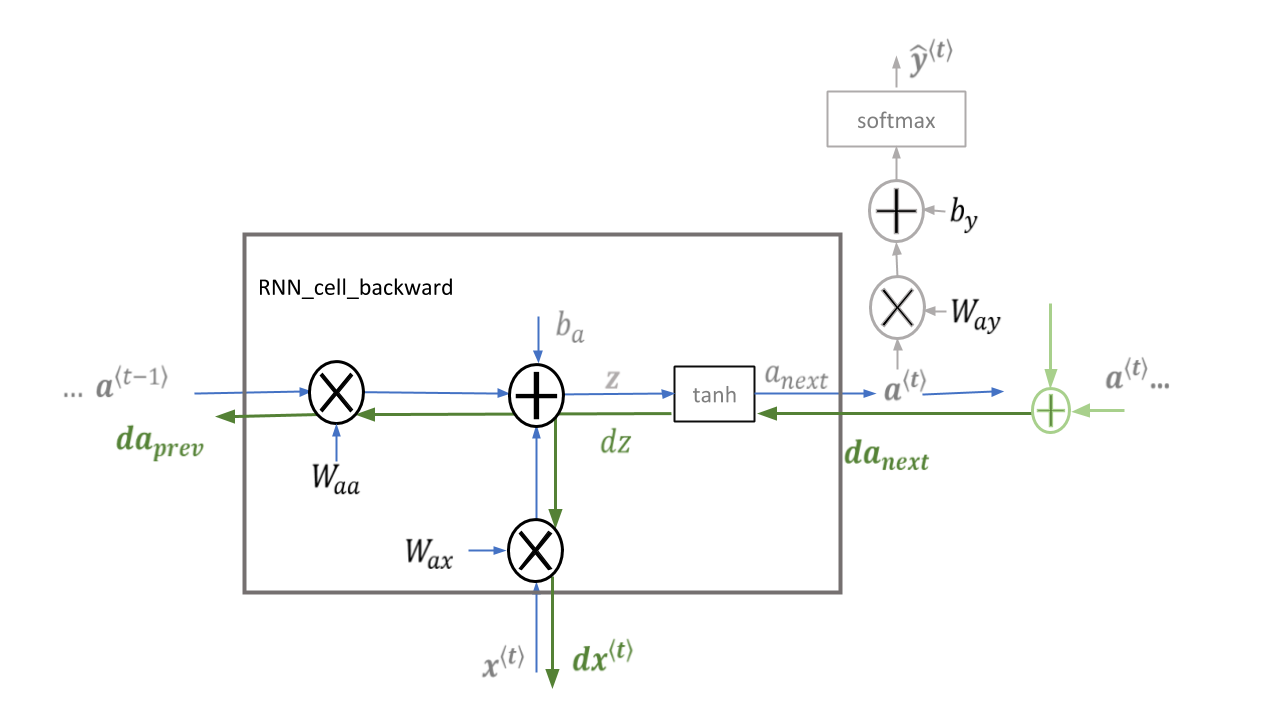
RNN的前向传播计算公式如下： \(a^{\langle t \rangle} = \tanh(W_{aa} a^{\langle t-1 \rangle} + W_{ax} x^{\langle t \rangle} + b_a) \\ \hat{y}^{\langle t \rangle} = softmax(W_{ya} a^{\langle t \rangle} + b_y) \tag{3.1}\)

假设这里我们已经得到了\(da_{next}\)，然后关注RNN Cell里面的计算细节。这个过程非常简单，先做如下计算分析：

• dZ：也就是标量对未激活值的梯度，这里需要通过\(da_{next}\)来计算。我们知道tanh函数的导函数为\(1-(tanh^2)\)。这里的tanh值实际上就是\(a_{next}\)。未激活值和激活值是一一对应的关系，也就是说，当未激活值\(z_{ij}\)发生\(\Delta z\)的变换，那么激活值中\(tanh(z_{ij})\)会发生\(1-(tanh(z_{ij})^2) \Delta z\)的变化，这就是说，激活值对未激活值的梯度也是一对一的，再考虑上标量对激活值的梯度，那么标量对未激活值的梯度就很显然了：\(dZ=da_{next}*(1-a_{next}^2))\)

• \(dW_{aa}\)：得到了dZ之后，结合之前标量对矩阵的求导的内容，就很容易得到标量对系数的梯度。

  \[dW_{aa} = dZ \cdot a^{<t-1>T}\] \[da_{prev} = W_{aa}^T \cdot dZ\] \[dW_{ax} = dZ \cdot x^{<t>T}\] \[dx^{<t>} = W_{ax}^T \cdot dZ\] \[dba = \sum_{batch}dZ\]

dtanh = da_next * (1 - a_next**2)  # 上文的dZ
dWaa = np.dot(dtanh, a_prev.T)
da_prev = np.dot(Waa.T, dtanh)
dWax = np.dot(dtanh, xt.T)
dxt = np.dot(Wax.T, dtanh)
dba = np.sum(dtanh, axis=1, keepdims=True)

LSTM Cell Backward

下图是LSTM Cell的前向和反向的计算过程示意图：

LSTM 前向的计算公式如下： \(\mathbf{\Gamma}_f^{\langle t \rangle} = \sigma(\mathbf{W}_f[\mathbf{a}^{\langle t-1 \rangle}, \mathbf{x}^{\langle t \rangle}] + \mathbf{b}_f) \tag{2.1}\)

Note

• sigmoid函数的导函数为：\(sigmoid(x)(1-sigmoid(x))\)
• tanh函数的导函数为：\(1-(\tanh^2(x))\)

假设这里我们已经获得了标量对激活值的梯度\(da_{next}\)以及标量对状态门的梯度\(dc_{next}\)，结合标量对矩阵的求导，梯度在激活函数之间的传播很容易对这个Cell的反向传播进行计算：

实际上，这里存在着这样的一组关系，注意到对\(c^{<t>}\)的梯度有两路，我们需要把这两路加和。为了防止\(dc_{next}\)的混淆，这里就不在使用下面的式子了。 \(dc_{next} = dc_{next} + da_{next} * \Gamma_o^{<t>} * (1-\tanh^2(c_{next})) \tag{3.x}\) 为了方便，这里不将激活函数的求导单步列出了： \(d\gamma_o^{\langle t \rangle} = da_{next}*\tanh(c_{next}) * \Gamma_o^{\langle t \rangle}*\left(1-\Gamma_o^{\langle t \rangle}\right) \tag{3.2}\)

有了上面的基础，这里我们就可以进一步求标量对系数的梯度了： \(dW_f = d\gamma_f^{\langle t \rangle} \begin{bmatrix} a_{prev} \\ x_t\end{bmatrix}^T \tag{3.6}\)

接着求标量对xt，a_prev，c_prev的梯度： \(dx^{\langle t \rangle} = W_f[:, n\_a:]^T d\gamma_f^{\langle t \rangle} + W_u[:, n\_a:]^T d\gamma_u^{\langle t \rangle}+ W_c[:, n\_a:]^T dp\widetilde c^{\langle t \rangle} + W_o[:, n\_a:]^T d\gamma_o^{\langle t \rangle} \tag{3.14}\)

伪码实现如下：

"""
Input: da_next, dc_next
"""

dot = da_next * np.tanh(c_next) * ot * (1-ot)
dcct = (dc_next + da_next * ot * (1-np.tanh(c_next)**2)) * it * (1-cct**2)
dit = (dc_next + da_next * ot * (1-np.tanh(c_next)**2)) * cct * it * (1-it)
dft = (dc_next + da_next * ot * (1-np.tanh(c_next)**2)) * c_prev * ft * (1-ft)

dWf = np.dot(dft, np.concatenate((a_prev, xt), axis=0).T)
dWi = np.dot(dit, np.concatenate((a_prev, xt), axis=0).T)
dWc = np.dot(dcct, np.concatenate((a_prev, xt), axis=0).T)
dWo = np.dot(dot, np.concatenate((a_prev, xt), axis=0).T)

dbf = np.sum(dft, axis=1, keepdims=True)
dbi = np.sum(dit, axis=1, keepdims=True)
dbc = np.sum(dcct, axis=1, keepdims=True)
dbo = np.sum(dot, axis=1, keepdims=True)

da_prev = np.dot(parameters["Wf"][:, :n_a].T, dft) + np.dot(parameters["Wi"][:, :n_a].T, dit) + np.dot(parameters["Wc"][:, :n_a].T, dcct) + np.dot(parameters["Wo"][:, :n_a].T, dot)

dc_prev = ft * (dc_next + da_next * ot * (1-np.tanh(c_next)**2))
dxt = np.dot(parameters["Wf"][:, n_a:].T, dft) + np.dot(parameters["Wi"][:, n_a:].T, dit) + np.dot(parameters["Wc"][:, n_a:].T, dcct) + np.dot(parameters["Wo"][:, n_a:].T, dot)